Code

The Codes for Defining, Constructing, and Using the de Bruijn graph for Genome Assembly ^[1]

The short read data are often stored in the fasta style file format. The content of each sequence starts with a ‘>’ symbol, the short read ID and the descriptions, followed by the actual sequence in the following lines.  

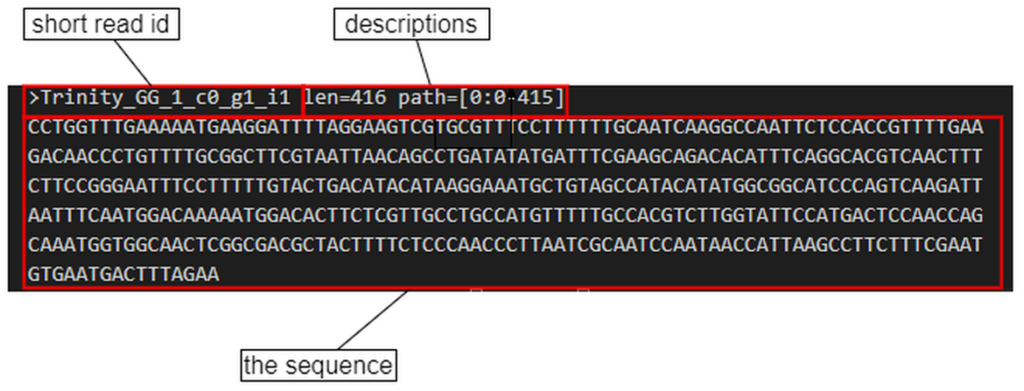
Fig. 1. The content of a sequence in a fasta file format.

With the short read sequences, we can start building the corresponding de Bruijn graph and reconstruct the contig sequence. The millipede genomes dataset that was used is in the fasta format, so we can generate an assembly with the code. To enhance the visualization, a mapping was created to map each short reads to its corresponding position at the output contig.

To construct the contigs from the short reads in def construct_graph, we first break the short reads into slices of length k, which forms the content in each node. The nodes are connected by a directed arrow. Then we find the contigs by def output_contigs with def find_start for finding the starting nodes. Since tracing down the de Bruijn graph will create many unwanted artifacts due to the reuse of nodes, we apply def find_contigs to map the short reads to the contigs to filter out the invalid contigs. 

Readers can refer to the Biopython seqIO package for more information: https://biopython.org/wiki/SeqIO

The following code in Python 3.7 is the low-level code for the de Bruijn graph definition, construction and contig finding:

from de_bruijn import *

def assembly(reads, k):
    """this function produces a list of assembly results 
        from a set of given sequencing reads

    Args:
        reads (List(String)): a list of strings of sequencing reads
        k (int): the string size for the de bruijn graph nodes

    Returns:
        final_contigs: a dictionary mapping the actual contigs 
        and their corresponding reads
    """
    vertices, edges = construct_graph(reads, k=k)
    contigs = output_contigs(vertices, edges)
    final_contigs = find_contigs(contigs, reads)
    
    return final_contigs, vertices, edges

These are the low level APIs used in the assembly function:

import copy

class Node:
    """ Class Node to represent a vertex in the de bruijn graph """
    def __init__(self, label):
        self.label = label
        self.indegree = 0
        self.outdegree = 0
        # self.from_read = set()
    
    def is_start(self):
        return self.outdegree > 0
    
class Edge:
    def __init__(self, label):
        self.label = label
    
    def __repr__(self):
        return f'{self.label}'

def find_start(V: dict):
    """Pick starting node (the vertex with zero in degree)

    Args:
        V (dict): a dictionary of Vertices with list(edges) as value

    Returns:
        start (Node): the Vertex to start the search
    """
    # initialize value of start
    start = [*V.keys()][0]
                    #[*V.keys()] unpack V.keys from dict_keys into a list
                    # so we can access it's first element using [*V.keys()][0]
    # mark start node as long as it has non-0 children 
    for k in V.keys():
        if V[k].outdegree > 0:
            start = k
                               
    # loop over the keys and pick the one with minimum in-degree
    for k in V.keys():
        if V[k].indegree < V[start].indegree and V[k].outdegree > 0:
            start = k
    return start

def construct_graph(reads, k):
    """ Construct de bruijn graph from sets of short reads with k length word"""
    edges = dict()
    vertices = dict()

    for id, read in enumerate(reads):
        i = 0
        while i+k < len(read):
            v1 = read[i:i+k]
            v2 = read[i+1:i+k+1]
            if v1 in edges.keys():
                vertices[v1].outdegree += 1
                edges[v1].append(Edge(v2))
            else:
                vertices[v1] = Node(v1)
                vertices[v1].outdegree += 1
                edges[v1] = [Edge(v2)]
                
            if v2 in edges.keys():
                vertices[v2].indegree += 1
            else:
                vertices[v2] = Node(v2)
                vertices[v2].indegree += 1
                edges[v2] = []
            
            i += 1

    return vertices, edges

def output_contigs(vertices, edges):
    """ 
    Perform searching for Eulerian path in the graph to output genome assembly
    """
    # V = vertices
    # E = edges
    V = copy.deepcopy(vertices)
    E = copy.deepcopy(edges)
    
    contigs = []
    # find all contigs
    while True:
        # Pick starting node (the vertex with zero in degree)
        start = find_start(V)
        # print(start)
        
        if not V[start].is_start():
        # if no nodes fulfill the start-node-requirement, end the function
            break 

        # Eulerian path algorithm
        # contig_id = 0
        contig = start
        current = start
        while len(E[current]) > 0:
            # Pick the next node to be traversed (for now, at random)

            next = E[current][0]
            del E[current][0]
                
            V[current].outdegree -= 1

            contig += next.label[-1]
            current = next.label
            V[current].indegree -= 1
        contigs.append(contig)
    return contigs

def find_contigs(contigs, reads):
    final_contigs = {}
    plot_count = 0
    read_len = len(reads)
    # sort the contigs, results will be in order from longest to shortest
    contigs.sort(key=lambda x: len(x), reverse=True)
    # Assume the longest contig is a major part in the assembly
    # map input into the contig
    
    for contig in contigs:
        if plot_count == read_len:
            break
        final_contigs[contig] = []
        for read in reads:
        # index is the starting position of the read's appearance in the contig
            index = contig.find(read) if index == -1:
                continue
            else:
                final_contigs[contig].append((read, index))
                plot_count += 1 # one more read-to-contig mapping is found
        
    
    return final_contigs

---

^[1]Part of the code (de Bruijn graph construction and trace back) is based on this python 2 implementation: https://github.com/mitbal/py-debruijn